Suppose I have a real symmetric $m \times m$ matrix $\Lambda$. This matrix is large ($m \gg 1$) and, for simplicity, we'll assume it's diagonal. I then construct a random $n \times n$ projection
$$ A = \frac{m}{n} \Phi^T \Lambda \Phi $$
where $\Phi$ is a random $m \times n$ matrix satisfying $\Phi^T \Phi = I_n$ and $m \gg n \gg 1$.
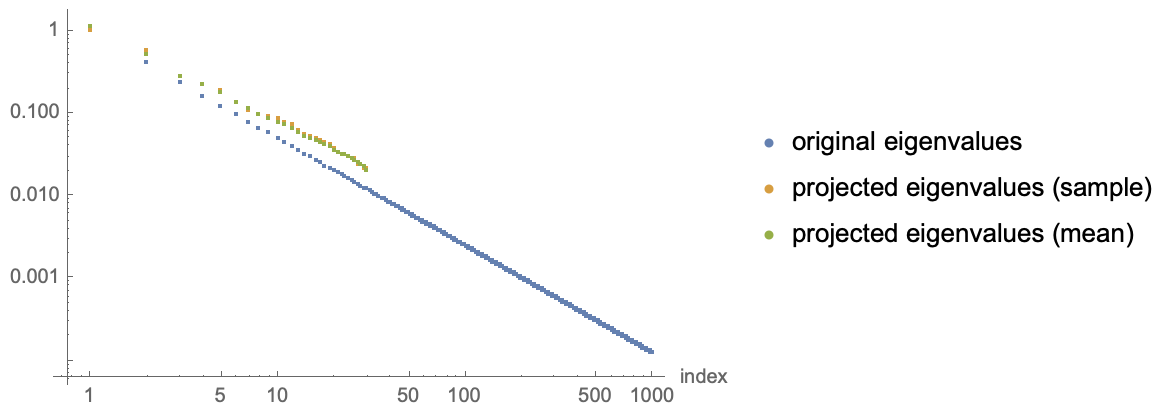
I am interested in understanding the typical eigenspectrum of the projected matrix $A$ in terms of the eigenvalues of $\Lambda$. This is for work in the spirit of statistical mechanics, and approximations or nonrigorous answers are perfectly fine. As an example of the sort of phenomenon I'd like to understand, I find numerically that when the eigenvalues of $\Lambda$ decay with index, the spectrum of $A$ approximately matches the top $n$ original eigenvalues, but with a systematic deviation that's roughly the same every trial (see plot below). How could I reach this conclusion analytically, and what is the form of the deviation? This seems likely to be tractable with tools from random matrix theory, but I wasn't able to find this problem in the literature.
Motivation
It turns out that this question is important in understanding the generalization behavior of infinitely-wide neural networks on e.g. image datasets. The original linear operator in question is actually the network's "neural tangent kernel." I do think the question of why one recovers the top $n$ eigenvalues is interesting in its own right, however.