11
$\begingroup$

A continuum is a compact, connected, metrizable space.

What are examples of continua that are contractible but nowhere locally connected, meaning that no point has a neighbourhood basis consisting of connected sets?

The following is an example of a contractible nowhere locally connected metrizable space, but I'm not aware of any compact examples (every segment on the "main line" has segments sticking out on a dense set).

the infinite infinite comb

This question was previously asked on MSE but didn't get an answer there.

Improve this question
$\endgroup$

1 Answer 1

Reset to default
8
$\begingroup$

An example of such a space was constructed by Edwards in "R. Edwards, A contractible, nowhere locally connected compactum, Abstracts A.M.S. 20 1999), 494.". The example is the following space:

Start with the space $X$ obtained stacking a sequence of Cantor fans (cones over the Cantor set) end to end as depicted.

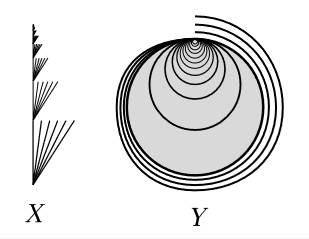
enter image description here

Then consider the space $X\times\Bbb R$, which looks like the upper half-plane with a lot of "fins" attached to it. Let $X'$ be the one point compactification of $X\times\Bbb R$, so that it looks like a closed disk with a lot of circular fins attached. The space $X'$ is a contractible continuum and it is locally connected precisely on the boundary of the circle. To make it nowhere locally connected construct $Y$ from $X'$ by wrapping one more Cantor fan around the circle, the resulting space is still contractible as explained here and clearly nowhere locally connected (in fact it is also nowhere connected im kleinen).

Now I'm wondering whether a planar contractible continuum must be locally connected somewhere, but that should be a separate question.

Improve this answer
$\endgroup$
4
  • $\begingroup$ This is a great example. I think it's worth noting that the contraction is not completely obvious. One cannot just contract the fan-surfaces onto the disk. It seems necessary to use the fact that a cone is well-pointed at its vertex. This allows one to put a sliver of surface between each of the fan surfaces in a way that does not change homotopy type. Then collapsing each of the fan-surfaces to a single circle will be a homotopy equivalence. After that one can perform the rotation contraction of the disk and the outer fan described in the other MO post. $\endgroup$
    – Jeremy Brazas
    Apr 14, 2022 at 3:28
  • $\begingroup$ I like it so much I illustrated it in 3-space here: wildtopology.com/bestiary/edwards-continuum $\endgroup$
    – Jeremy Brazas
    Apr 14, 2022 at 3:45
  • $\begingroup$ @JeremyBrazas Those are some beautiful images! How did you generate them? Unrelated but I'm glad you wrote a blog post about this space, now I can keep postponing to "tomorrow" the topology blog I've been meaning to start writing for years! $\endgroup$
    – Alessandro Codenotti
    Apr 14, 2022 at 11:50
  • $\begingroup$ Thanks! I worked out the transformational geometry to plot the various parts as parameterized curves and surfaces in mathematica. $\endgroup$
    – Jeremy Brazas
    Apr 14, 2022 at 15:57

Your Answer

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.

Not the answer you're looking for? Browse other questions tagged or ask your own question.