0
$\begingroup$

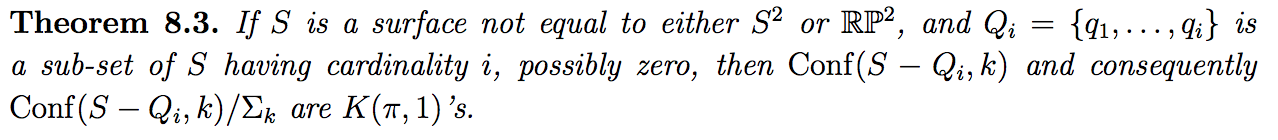
From the lecture notes INTRODUCTION TO CONFIGURATION SPACES AND THEIR APPLICATIONS, p. 18, I find: enter image description here

Os it possible to derive the cohomology ring $H^*(Conf(S,k)/\Sigma_k;\mathbb{Z}_2)$ from the above theorem?

Question 1: Given a surface $S$, are there any methods to compute the fundamental group of $k$-th unordered configuration space $$ \pi_1(Conf(S,k)/\Sigma_k)? $$

Question 2: Given a group $G=\pi_1(Conf(S,k)/\Sigma_k)$, I find $ K(G,1)=BG. $ Are there any methods to compute the cohomology ring (cup product structure) $$ H^*(BG;\mathbb{Z}_2)? $$

Improve this question
$\endgroup$

1 Answer 1

Reset to default
1
$\begingroup$
  • Question 1 Yes, at least up to extension problem. The proof of the fact that $Conf(S-Q_k,k)$ is $K(\pi ,1)$ provides an explicit decomposition of $Conf(S-Q_k,k)$ into a fibration of $K(\pi ',1)$'s.
  • Question 2 Yes, at least in theory. One can use the isomorphism $$H^*(BG,k)\cong Ext ^*_{k[G]}(k,k)$$ and the product structure of $Ext$ groups. However, in practice this method is not very convenient, you would be better off to look for some ad-hoc method.
Improve this answer
$\endgroup$

Your Answer

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.